Algoritmos y Estructura de Datos

Arboles de expansion minima (Algoritmos de Kruskal y Prim)

Árboles de recubrimiento mínimo

Un problema donde aplicar el algoritmo voraz es el de obtener el árbol de recubrimiento mínimo en un grafo conexo no dirigido. Ese árbol es un subgrafo que conecta todos los nodos siguiendo un camino cuyo coste de la suma del valor de las aristas es mínimo

El subgrafo obtenido contiene los 5 nodos del grafo unidos por 4 aristas. Hay que recordar que un grafo conexo con n nodos debe contener al menos n-1 aristas. Si contiene menos no es conexo. Si contiene más existe al menos un ciclo. En otro caso si contiene exactamente n-1 aristas ese subgrafo es un árbol pues es conexo y no contiene ciclos.

Este planteamiento se aplica en problemas reales. Supongamos que cada nodo representa una ciudad y queremos tender un cable teléfonico que conecte todas las ciudades usando la menor longitud de cable. Los valores de las aristas son las distancias entre ciudades pasando por lugares por donde podríamos instalar ese cable, como carreteras. Buscando el árbol de recubrimiento mínimo obtendríamos la menor distancia que conecta todas las ciudades.

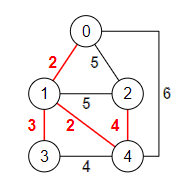
El algoritmo de Kruskal

Para ver si la selección de una arista es completable hemos de comprobar si una arista que se agregue al resultado formará un árbol. Para conseguirlo aplicaremos la particularidad del algoritmo de Kruskal, que se basa en usar una estructura de partición o de conjuntos disjuntos.

Antes de exponer el código hemos de decir que usamos una estructura para representar un grafo tal como se expone en la herramienta Web Tools online: Grafos. Para el grafo de ejemplo que hemos estado usando en los apartados anteriores, la estructura es la siguiente:

                [{"index":0, "parent":-1},
                {"index":1, "parent":
                    [{"index":0, "value":2}]
                },
                {"index":2, "parent":
                    [{"index":0, "value":5},
                    {"index":1, "value":5}]
                },
                {"index":3, "parent":
                    [{"index":1, "value":3},
                    {"index":4, "value":4}]
                },
                {"index":4, "parent":
                    [{"index":1, "value":2},
                    {"index":2, "value":4},
                    {"index":0, "value":6}]
                }]
            

Cada nodo se identifica con un índice index. Aunque en la herramienta para editar grafos se permiten índices enteros no negativos cualesquiera, no necesariamente correlativos, para aplicar la estructura de partición necesitamos que sean correlativos empezando en cero.

Cada nodo tiene obligatoriamente uno o más enlaces que configuran aristas a otros nodos. Estos enlaces se incluyen en un array en parent. Uno de los nodos es el inicial y le asignamos -1. Para el resto configuramos los enlaces sin tener en cuenta el sentido del enlace en el caso de que querramos un grafo no dirigido, como es el caso. El valor de la arista se indica en value. Pueden incluirse otras propiedades opcionales como lineOffset o lineTextOffset que sirven para la presentación visual del grafo, no interviniendo en la estructura básica que necesitamos para este caso. Conocido lo anterior veamos ahora la implementación en JavaScript del algoritmo de Kruskal.

                function kruskal(nodos=[]){
                    let aristas = {};
                    for (let nodo of nodos){
                        if (Array.isArray(nodo.parent)){
                            for (let link of nodo.parent){
                                if (typeof link==="object" && link.hasOwnProperty("value")){
                                    aristas[`${nodo.index},${link.index}`] = link.value;
                                }
                            }
                        }
                    }
                    let aristasEnOrden = Object.keys(aristas).sort((a,b) => aristas[a]-aristas[b]);
                    let conjuntosIniciales = nodos.map(v => [v.index]);
                    let [rotulos, rangos, elementos] = construir(conjuntosIniciales);
                    let rotulo1, rotulo2;
                    let resultado = [];
                    for (let arista of aristasEnOrden){
                        let [index1, index2] = arista.split(/,/).map(v => +v);
                        [rotulo1, rotulos] = buscar(rotulos, index1);
                        [rotulo2, rotulos] = buscar(rotulos, index2);
                        if (rotulo1 !== rotulo2){
                            [rotulos, rangos] = fusionar(rotulos, rangos, rotulo1, rotulo2);
                            resultado.push(arista);
                            if (resultado.length === nodos.length-1) break;
                        }
                    }
                    return resultado;
                }
            

Algoritmo de Prim

Con el algoritmo de Kruskal iterábamos por las aristas ordenadas por su valor creciente. Se iban formando subárboles no conectados entre sí a medida que avanzábamos por el bucle voraz. Si en el ejemplo interactivo del apartado anterior ejecuta el "Ejemplo 2", verá que en la iteración que selecciona la cuarta arista obtenemos el resultado parcial ["1,0", "2,1", "4,3", "6,5"].

Otra forma de construir el árbol de recubrimiento mínimo es usando el algoritmo de Prim. En este caso no se ordenan las aristas. Vamos iterando por ellas haciendo una selección de proximidad a un nodo elegido, normalmente el primer nodo. A medida que el bucle voraz avanza, el árbol va creciendo de forma unificada hasta completar todos los nodos. Para el grafo anterior se van formando las aristas partiendo del nodo raíz 0. Cuando se agrega una nueva arista está conectada con alguna de las aristas ya existentes en el subárbol, como se muestra en la siguiente evolución del array de resultado:

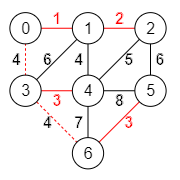
                i Resultado
                --------------------------------------
                1 ["1,0"]
                2 ["1,0","2,1"]
                3 ["1,0","2,1","3,0"]
                4 ["1,0","2,1","3,0","4,3"]
                5 ["1,0","2,1","3,0","4,3","6,3"]
                6 ["1,0","2,1","3,0","4,3","6,3","5,6"]
            

El bucle voraz finalizará cuando A contenga todos los nodos de N. La función para seleccionar un candidato es en este caso también completable. Al seleccionar un nodo, éste debe ya completar la solución. La selección debe obtener una arista formada por la pareja de nodos [x, y] de menor longitud, de tal forma que x ∈ A, y ∈ N-A. Agregamos el nodo y al conjunto A y la arista [x, y] al resultado.

Veamos una implementación práctica donde no es necesario declarar el conjunto A, aunque está implícito en la ejecución. El código del algoritmo y el ejemplo interactivo se exponene a continuación. Luego explicaremos paso a paso la ejecución.

                function prim(nodes=[]){
                    let n = nodes.length;
                    let longitudesAristas = Array.from({length:n}, () =>
                        Array.from({length:n}, () => Infinity));
                    for (let node of nodes){
                        if (Array.isArray(node.parent)){
                            for (let link of node.parent){
                                if (typeof link==="object" && link.hasOwnProperty("value")){
                                    longitudesAristas[node.index][link.index] = link.value;
                                    longitudesAristas[link.index][node.index] = link.value;
                                }
                            }
                        }
                    }
                    let masProximo = [];
                    let distanciaMinima = [];
                    for (let i=0; i< n; i++){
                        masProximo[i] = 0;
                        distanciaMinima[i] = longitudesAristas[i][0];
                    }
                    let resultado = [];
                    for (let i=1; i< n; i++){
                        let minimo = Infinity;
                        let k;
                        for (let j=1; j< n; j++){
                            if (distanciaMinima[j]>=0 && distanciaMinima[j]< minimo){
                                minimo = distanciaMinima[j];
                                k = j;
                            }
                        }
                        resultado.push(`${k},${masProximo[k]}`);
                        distanciaMinima[k] = -1;
                        for (let j=1; j< n; j++){
                            if (longitudesAristas[j][k]< distanciaMinima[j]){
                                distanciaMinima[j] = longitudesAristas[j][k];
                                masProximo[j] = k;
                            }
                        }
                    }
                    return resultado;
                }
            

Link de apoyo

Algoritmo de Kruskal e Implementacion en C++

Algoritmos de Kruskal y Prim en JavaScript

Aplicación informática KPTS (Kruskal, Prim, Tabu Search)